Manipulons la figure...
L'animation illustre le principe de la suspension d'un véhicule automobile
La suspension est modélisée par l'association d'un ressort (raideur k) et d'un amortisseur (coefficient de frottement fluide h), soumis à une excitation due aux aspérités de la chaussée. La vitesse du véhicule impose la fréquence de l'excitation.
Il y a un système semblable pour chaque roue.
Appelons : m la masse, k la raideur du ressort, l sa longueur et h le coefficient de frottement fluide de l'amortisseur.
L'équation du mouvement s'écrit, par application du Principe Fondamental de la Dynamique dans un référentiel fixe :
mx" =-h*(x'-y') - k*(x-y), si on désigne par x(t) le mouvement du châssis et y(t) le relief du sol défilant sous la roue (alors x-y représente l'allongement du ressort par rapport à l'équilibre).
En d'autres termes, on peut écrire :
![]()
avec les notations suivantes :
- ω0 =√(k/m) : pulsation propre de l'oscillateur (dépend de la masse et de la raideur du ressort). Elle diminue avec le chargement du véhicule.
- Q = √(km)/h : facteur de qualité, dans lequel interviennent les 3 paramètres du système. Il augmente avec le chargement.
Voir cette page pour l'équation différentielle et celle-là pour l'animation du régime libre d'un oscillateur amorti.
Manipulation :
Choisir le relief du sol en cliquant sur un des panneaux routiers.
Des curseurs permettent de faire varier :
- la vitesse du véhicule
- le facteur de qualité Q0 du véhicule à vide.
- la charge, en pourcentage de la masse du véhicule.
Deux graphes montrent les oscillations du châssis et du sol. On peut les faire glisser l'un sur l'autre afin de les comparer. Le bouton clear permet de les réinitialiser.
Le diagramme de gain (amplitude de l'oscillation/amplitude de l'excitation) est représenté en haut et à droite. Pour plus de précision et pour visualiser la phase, voir l'analogie électrique ci-dessous.
En faisant varier l'excitation de cet oscillateur : route plate, marche d'escalier, "tôle ondulée", bosse, on peut observer le régime libre, le régime sinusoïdal forcé, etc.
Examiner le rôle de la charge du véhicule, en particulier sur le courbe de gain.
Examiner le rôle de la vitesse du véhicule, et constater l'existence d'une vitesse critique...
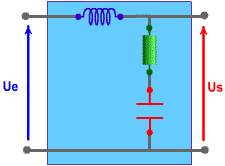
Analogie électrique :
La fonction de transfert complexe en régime sinusoïdal forcé s'écrit, en nommant W la pulsation réduite :
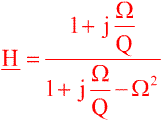 |
|
 |