Manipulons la figure...
L'animation illustre le principe d'un oscillateur paramétrique.
Le Botafumeiro est un gigantesque encensoir, suspendu au plafond de la cathédrale de Saint Jacques de Compostelle. Son oscillation permet de diffuser de l'encens dans toute la cathédrale.
Sa suspension a la particularité d'être de longueur variable, grâce à un ensemble de cordes tirées à la main par 8 hommes.
Ce système constitue un pendule pesant de longueur variable.
Etude mécanique
Le Théorème du Moment Cinétique appliqué à la masse donne, en projection sur l'axe de rotation :
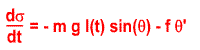
- σ est le moment cinétique par rapport à l'axe de rotation : σ = m l² θ'
- m est la masse
- l est la longueur du fil (jusqu'au centre de gravité du pendule)
- θ est l'angle de rotation par rapport à la verticale
- θ' est la vitesse angulaire
- f est le coefficient du couple de frottement
on obtient l'équation différentielle :
θ" +((2l'+f)/l) θ' + ω02 sin(θ) = 0
ω0 est la pulsation propre du pendule (ω02= g/l)
On éliminant le frottement et en supposant que les oscillations restent petites (!), l'équation se simplifie :
θ" + 2 (l'/l) θ' + ω02θ = 0
dans cette équation le "terme résistant" (l'/l) devient négatif lorsque la corde se raccourcit (l'<0) : cela correspond à un apport d'énergie par les personnes qui tirent la corde, et cet apport d'énergie se traduit par une augmentation de l'amplitude des oscillations. Mais pour que la corde puisse être raccourcie, il faut également l'allonger ! Dans un cycle d'oscillation, il faut donc "pomper", en choisissant le moment opportun pour allonger ou raccourcir la corde. Le maximum d'efficacité s'obtient si l'on tire quand la corde est à la verticale, et l'on la relâche quand la vitesse s'annule (deux cycles de pompage par période).
- Cette "excitation" est réalisée de la même manière lorsqu'on se balance sur une balançoire de type "escarpolette", ou lorque des acrobates s'élancent sur le trapèze.
Mode d'emploi
L'animation permet de choisir 2 modes de variation de l(t) :
- mode sinusoïdal, à l'aide d'une poulie ayant un picot excentré : on peut alors choisir la fréquence de variation de l(t).
- mode manuel : on tire sur la corde à l'aide de la souris (cliquer-glisser sur la main).
On peut stopper le pendule et lui redonner une autre position initiale, en choisissant l'instant auquel on relâche.
Il est possible de mettre du frottement et d'en faire varier le coefficient.
Un bouton permet d'immobiliser le pendule. Pour le relancer, cliquer-glisser sur l'encensoir.
Deux graphes montrent la variation de longueur de la corde, et l'angle de rotation du pendule. On peut les superposer pour les comparer. Un bouton permet de les effacer.
Manipulation
- En mode sinusoïdal et avec la fréquence de départ (2 ω0), on constate que l'amplitude des oscillations augmente, puis diminue, et ceci de manière périodique. Cela s'explique par le fait que la période du pendule augmente, brisant ainsi le phénomène de résonance qui s'est installé. Mais cette résonance "accroche" à nouveau lorsque l'amplitude diminue, car alors la période diminue également, etc...
Modifier la fréquence pour voir comment il est possible d'augmenter l'amplitude des oscillations.
- En mode manuel, et en manoeuvrant habilement, on peut rapidement amplifier le mouvement. Essayer de faire faire à l'encensoir le tour complet !